「POJ-3494」Largest Submatrix of All 1’s(单调栈)

发表于 | 分类于 ，

「POJ-3494」Largest Submatrix of All 1’s
单调栈，寻找01矩阵中最大的元素全为1的子矩阵

题意

给定一个$m×n$的$01$矩阵，求只包含元素$1$的最大子矩阵。

对于每一组输入，输出最大全$1$子矩阵的元素数目。

思路

这题的暴力解法，即对于图中的每一个点$(i,j)$,枚举其右下方的每一个点，检测自$(i,j)$到$(x,y)$组成的子矩阵元素是否全为1.复杂度为$O(n^3m^3)$.

显然我们需要优化复杂度。

对于如下矩阵：

$$
\begin{vmatrix}
0 & 1 & 0 & 1 & 0\
0 & 1 &1 & 0 & 0\
1 & 1 & 1 & 0 & 0\
0 & 0 & 0 & 0 &1\
\end{vmatrix}
$$
枚举每行元素

1533815577042

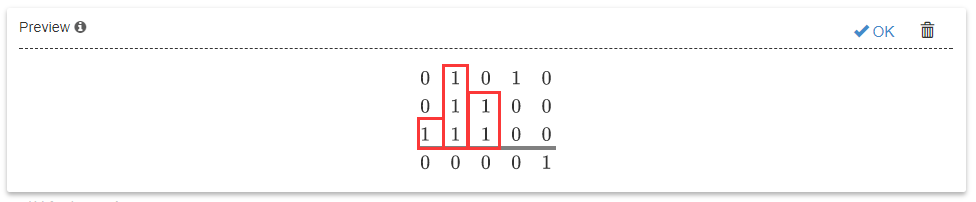
1533815742193

1533815953866

1533816076001

即对于矩阵的每一行，枚举以每一行为底，柱状图所能形成的最大矩形面积，所有行中的最大值即为答案。

问题转化为

POJ2559 Largest Rectangle in a Histogram

img

解法

基于原矩阵，构造一个新矩阵
$$
\begin{matrix}
0 & 1 & 0 & 1 & 0\
0 & 2 & 1 & 0 & 0\
1 & 3 & 2 & 0 & 0\
0 & 0 & 0 & 0 &1\
\end{matrix}
$$
对于每一行，套用POJ2559的方法，使用单调栈求解当前行的最大值，再遍历求出总的最大值即可。

POJ2559 最大矩形面积

对于最大矩形面积，我们需要找到每一个柱状块向左、右所能扩展的区间的最大长度。即，区间内的柱状块高度都不小于起始柱状块的高度。

使用单调栈维护一个从起点到当前点的单调递增序列，如果栈顶元素的高度大于当前点，弹出栈顶元素，直到栈为空，或栈顶元素小于当前点，以此来维护栈的递增性。

我们需要证明，之前弹出的元素对之后的点没有影响，即$i$之前大于$h[i]$的元素，必然不是$h[i+1]$的扩展边界：

  • 若$h[i]<h[i+1]$，点$i+1$ 显然无法向左继续扩展，边界为$h[i]$

  • 若$h[i]≥h[i+1]$，之前出栈的点一定大于$h[i]$，不影响$i+1$向左继续扩展

以上结论具有递推性，可用数学归纳法证明。

由此我们可以线性求出每个元素向左、右扩展形成的最大矩形面积，即s[i]=(l[i]+r[i]+1)*h[i]

Code|Solution to POJ 2559

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <cstdio>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <stack>
using namespace std;

const int maxn=2000+10;
int a[maxn][maxn],l[maxn],r[maxn];

int main()
{
    int n,m,x;
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        memset(a,0,sizeof(a));
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=m;j++)
            {
                scanf("%d",&x);
                if(x) a[i][j]=a[i-1][j]+1;
                else a[i][j]=0;
            }
        }
        int ans=0;
        for(int i=1;i<=n;i++)
        {
            stack<int> st;
            for(int j=1;j<=m;j++)
            {
                while(!st.empty()&&a[i][st.top()]>=a[i][j]) st.pop();
                int res=0;
                if(!st.empty()) res=st.top();
                st.push(j);
                l[j]=(j-1-res)*a[i][j];
            }
            while(!st.empty()) st.pop();
            for(int j=n;j>0;j--)
            {
                while(!st.empty()&&a[i][st.top()]>=a[i][j]) st.pop();
                int res=n;
                if(!st.empty()) res=st.top()-1;
                st.push(j);
                r[j]=(res-j)*a[i][j];
            }
            for(int j=1;j<=m;j++)
                ans=max(ans,l[j]+r[j]+a[i][j]);
        }
        printf("%d\n",ans);
    }
    return 0;
}