「BZOJ-3732」Network (Kruskal重构树)

发表于 | 分类于 ，

BZOJ3732-Network
给定一个无向图，求图中A点到B点的所有路径中，最长边的最小值

思路

可以直接求出最小生成树，答案即为a到b路径上的最小边权，用LCA 求解。

此处采用Kruskal重构树求解。

Kruskal重构树

在Kruskal算法中，当找到两个不属于同一集合的联通块（子树）时，我们直接用边将两联通块相连，从而构建出最小生成树。

在Kruskal重构树中，对于两个不属于同一集合的联通块，我们首先建立一个虚点，作为两个子树的父节点，让两个子树的根节点与虚点相连，即可构造Kruskal重构树。虚点的点权即为原边的边权。

通过这一性质，我们成功将最小生成树上的路径信息转化成了点权信息。

解法

Kruskal重构树的构建过程如下：

  1. 将边对于边权从小到大进行排序；

  2. 遍历边集，用并查集维护两点的连通性，若祖先不相同，则建立一个权值为边权的节点，其左右儿子分别为两个点的祖先节点，并将当前点设为两联通块的根节点；
    img

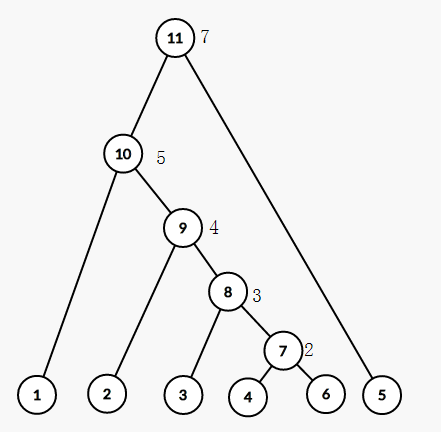
对于构建完成的Kruskal重构树，对u,v求其LCA的点权即为所求解。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <cmath>

using namespace std;

const int maxn=3e5+10;

struct Edge
{
	int u,v,w;
	bool operator <(const Edge e) const {
		return w<e.w;
	}
}es[maxn];

int n,pre[maxn],val[maxn];

int Find(int x) {return x==pre[x]?x:pre[x]=Find(pre[x]); }

vector<int> tree[maxn];

void add(int u,int v)
{
	tree[u].push_back(v);
	pre[v]=u;
}

int dep[maxn],fa[maxn][30];

void dfs(int u,int pre)	//预处理各节点深度+初始fa[u][0]
{
	dep[u]=dep[pre]+1;
	fa[u][0]=pre;
	for(int i=0;i<tree[u].size();i++)
	{
		int v=tree[u][i];
		if(v!=pre) dfs(v,u);
	}
}

void init()	//预处理fa数组
{
	for(int i=1;(1<<i)<=n;i++)
		for(int u=1;u<=n;u++)
			fa[u][i]=fa[fa[u][i-1]][i-1];
}

/**************求LCA(u,v)**************/

int LCA(int u,int v)
{

	if(dep[u]<dep[v])
		swap(u,v);

	int d=dep[u]-dep[v];
	for(int i=0;(1<<i)<=d;i++)	//将u上调d个距离
		if((1<<i)&d) u=fa[u][i];

	if(u==v) return u;	//特判此时u,v是否在同一位置，如果是，u,v都在LCA上

	for(int i=(int)log(n);i>=0;i--)	//同时上调u,v
	{
		if(fa[u][i]!=fa[v][i])
		{
			u=fa[u][i];
			v=fa[v][i];
		}
	}
	return fa[u][0];	//最后会使u,v成为LCA的子节点
}

int main()
{
	int m,k,u,v,w;
	scanf("%d%d%d",&n,&m,&k);
	for(int i=1;i<=2*n;i++) pre[i]=i;
	for(int i=0;i<m;i++)
		scanf("%d%d%d", &es[i].u, &es[i].v, &es[i].w);
	sort(es,es+m);
	int index=n,lim=n<<1;
	for(int i=0;i<m;i++)
	{
		u=es[i].u,v=es[i].v,w=es[i].w;
		int fx=Find(u),fy=Find(v);
		if(fx==fy) continue;
		index++;
		add(index,fx);
		add(index,fy);
		val[index]=w;
		if(index==lim-1) break;
	}
	dep[0]=0;
	n=index;
	dfs(index,0);
	init();
	while(k--)
	{
		scanf("%d%d",&u,&v);
		printf("%d\n",val[LCA(u,v)]);
	}
	return 0;
}